

Optar stands for OPTical ARchiver. It's a codec for encoding data on paper or free software 2D barcode in other words. Optar fits 200kB on an A4 page, then you print it with a laser printer. If you want to read the recording, scan it with a scanner and feed into the decoder program. A practical level of reliability is ensured using forward error correction code (FEC). Automated processing of page batches facilitates storage of files larger than 200kB.
optar.tgz - unpack this source code and see README for instructions. Contains encoder optar and decoder unoptar. Works with PGM (Portable GrayMap) uncompressed picture format.
If you wish to change the resolution - for example half the resultion, 1/4 data or 50 kB per page - edit optar.h and change
#define XCROSSES 65 /* Number of crosses horizontally */ #define YCROSSES 93 /* Number of crosses vertically */
to approximately a half:
#define XCROSSES 32 /* Number of crosses horizontally */ #define YCROSSES 46 /* Number of crosses vertically */
Then do "make clean" and compile and install Optar again. You can reduce or increase these numbers according to the overall resolution of your printer and scanner combination.
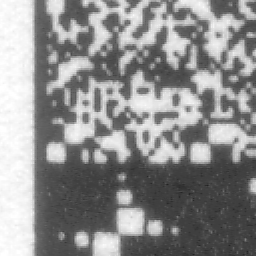
I tried ordinary office paper, laser printer hp LaserJet 2200dtn and scanner CanoScan N650U at 1200dpi weighted with yellow pages. The data density was default 200kB per page. I folded the paper twice, put it into my pocket, pulled out and scanned. Quality of the acquired image can be seen on the right. Resulting Golay statistics show very high reliability:
| Bad bits | Count [Golay codewords] |
| 0 | 132814 |
| 1 | 368 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
Extrapolation estimate of the probability in the last row (1/(386*(386/132814)^3)) suggests that one Golay symbol with 4 bad bits, which means data damage, occurs once in 105,531 (hundred thousand...) pages.

The printer, although having 600dpi nominal resolution, cannot reliably print individual white and black dots with 600dpi. The practical limit is at 200dpi, i. e. 3x3 pixel squares. That corresponds to 200kB per page when taking overhead into account.
Error correction. Even at those 200dpi, the dots are unreliable. The paper surface is rough, the edges of the black are jagged and bleed, the black is not uniformly black, there are specks of stray toner or some dots peel off. There are pieces of black and white dirt coming into contact with the paper. Some effects can be canceled by software - thin pieces of dust, crosstalk between neighbouring pixels, black edge bleed, certain level of scanner noise. The rest cannot be canceled and is often difficult to judge by human eye. These cases create readout errors. Error correcting codes are used to reduce the error probability to a practically negligible level. Currently it's Golay code which can fix 3 bad bits in each 24-bit code word. Each 24 bit code word however carries only 12 bits of payload, the remaining 12 bits are guard against these three errors. If 4 bits get flipped, this situation is detected and reported, but cannot be corrected. If more, the outcome is uncertain.
Previously, Hamming codes 16:11 and 8:4 were used, but they don't offer such robustness against errors. Generally, the error rate however drops with increasing pixel size, so they can be used for smaller capacity per page.
Since a piece of dust could cover easily 4 neighbouring pixels and create an irreparable Golay symbol error with otherwise low error rate, the bits are spread. The image is divided into 24 strips, each strip carries only certain bit position of all Golay codes.
Synchronization. The paper slightly deforms and the laser printer feed or scanner motion can slip, causing deformed image. The bit mesh is so fine that it would desynchronize by several pixels in the middle of the paper and read out complete bullshit. Therefore there is a regular mesh of crashtest dummy style checkerboard crosses that are synchronized on precisely by the decoding software using convolution with the cross pattern. This sync is then rerun with subpixel precision to get maximum readout reliability.
Border. It is necessary to determine the precise position of the recording corners, even if the recording is stretched, sheared, rotated or shifted. Therefore there is a border around the recording, couple of pixels wide.
When determining the corners, a false positive could be caused by a piece of black dirt sitting in the corner of the white border. That would cause the whole recording to be read out as total bullshit. Therefore there is an algorithm to remove such dirt, which uses the fact that the border around the recording is continuos. The border has to be thick enough to not get interrupted by a casual piece of white dirt.
This algorithm first performs a floodfill on the white border from 8 seeds in the corners and middles of the edges. Then a floodfill is performed on area which was not yet floodfilled with seed in the middle of the picture. This floodfills the recording area. The dirts in the border stay unfilled out. Then all the places that were not yet floodfilled are whitened out - this removes the dirts. The reliability of corner detection is then ensured.
To make sure the Golay code is not programmed with a mistake, I first needed to understand it. Starting with a predefined table of zeroes and ones doesn't count as understanding so I found an article (now a book without free text) called Decoding the Golay code by hand, which describes the principle of Golay code in an easy to remember way.
According to this article, Golay code consists of 12 data bits and 12 parity bits. First the data bits are painted on a dodecahedron (12 faces). Then a paper mask of 5 faces into a circle with a hole in the middle is applied with the hole on each of the face. All visible bits are XORed together and written as parity symbol for that nth position. The the data word and parity word are concatenated. This creates 4096 Golay words. Each two 24 bit Golay words differ in at least 8 bits. Therefore if up to 3 bits are altered, we still know for sure the original code word.
The decoding is implemented in Twibright Optar in a primitive way. A table of words is scanned until a match with up to 3 different bits is found. If no match is found, then the Golay word must be irreparably damaged. It's possible to decode faster, it's just not implemented.